If you understand compounding—the idea that interest grows on interest—you probably already know more about money and how to build wealth than 90% of the population.

And you will have at your disposal a weapons-grade tool to help you reach Financial Independence because compounding is the bedrock of any serious long-term investment strategy.

It is so fundamental to Financial Independence that Albert Einstein once quipped:

“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it.”

Legendary investor, Warren Buffett, has also spoken of compounding’s awesome powers:

"My wealth has come from a combination of living in America, some lucky genes, and compound interest."

What’s so special about compounding? Why did Einstein call compound interest the Eighth Wonder of the World? And why did Buffett attribute his wealth in large part to compound interest?

They did so because they were aware of a mysterious and magical property of compounding: Exponential Growth.

Consider the following:

It is believed that Peter Minuit bought the island of Manhattan from the Lenape, a Native American tribe, in 1626 for $24.

Now suppose the Lenape invested their profits ($24) and could have earned a 7% annual interest rate each year up until present day 2017.

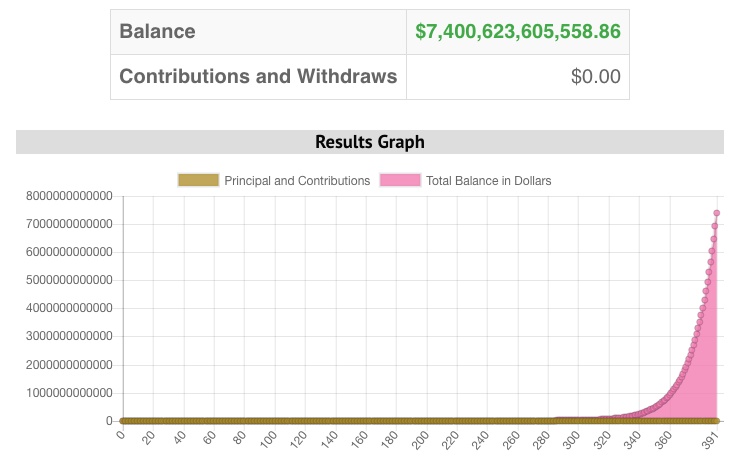
How much do you think the Lenape would have today if they let their initial $24 investment grow and compound for all these 391 years?

A: ~$700M - Millons ($7,000,000)

B: ~$700B - Billions ($7,000,000,000)

C: ~$7T - Trillions ($7,000,000,000,000)

The answer is C!

A $24 dollar investment would have ballooned into $7 trillion dollars! (The actual amount being $7,400,623,605,558.86). For some perspective look at the 7 towering over the 24:

$7,000,000,000,024.00

This is a mathematical miracle. One that Einstein considered “the greatest mathematical discovery of all time.” And namely, thanks to:

Exponential Growth.

This chart demonstrates exponential growth. That’s what you want your money to do.

Compute it yourself using Wealth Meta’s compound interest calculator.

A sum of money which compounds over time, will inevitably and ruthlessly take on the behavior of exponential growth. Which means, if your money starts off as a drop of water, it will soon enough multiply into a glass of water, a bucket of water, a pool, a lake, a Great Lake, and then into an ocean. And all the while, you’re swimming in Financial Freedom (assuming you’ve kept your investment fees low and have stayed out of debt.)

Compounding can make you rich. And it does so because of exponential growth.

And you don’t need to wait 391 years like the Lenape to see impressive growth because compounding can give you a handsome nest egg on a more a realistic timeline. Take the following scenarios, all of which assume an average annual interest rate of 7%:

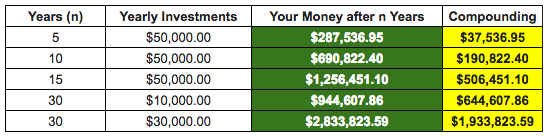
Depending on your expenses, these are retirement-level sums. “How can anyone retire on less than $300,000?,” you ask. If your expenses are $12,000 per year (which in a country like Colombia is enough), invest in low-cost funds, and follow a 4% withdrawal rate strategy, it’s possible to retire once you’ve accumulated $300,000.

In any case, increase the time (n), interest rate, and/or investment amounts, and you have even more money at the end of n years. See our compound interest calculator to play around with your own numbers.

What is compounding exactly?

Compounding is the idea that interest grows on interest. Money that earns money. (Where interest comes from and how it works is a discussion for another day.)

The process goes something like this:

1. You deposit $100 in the bank. This is your principal.
2. Let’s say the bank pays you a 10% annual interest rate (Yes, yes that's unrealistic. This is just an example.)
3. Thus, after Year 1, you have $110.
4. Your initial deposit ($100) is bundled together with the interest ($10) to become your new principal. Which means, the bank doesn’t differentiate between the initial deposit and the interest. In the bank’s eyes, $110 is now your balance and in the next year you’ll earn interest on it. As far as you’re concerned, that $10 in interest is the closest thing you’ll find to money growing on trees.
5. Now, after Year 2, you’ll have $121 (as opposed to $120) because the bank paid you 10% interest on the initial principal and the interest (=$110). This is compounding.

That extra dollar ($120 to $121) is compounding and over time will grow exponentially. It is responsible for this “Roger, we’re ready for take-off” curve.

In addition to interest-bearing bank accounts, you can seek out compounding returns in bonds (and bond funds), which pay coupons, and dividend-paying stocks (and stock funds).

Remember, however, what Einstein said about compounding:

“He who understands it, earns it … he who doesn’t … pays it.”

Einstein is talking about debt. Compounding can likewise work against you because whenever you assume debt—a loan, a mortgage, credit card interest—you pay the bank interest - often compounded interest.

And because you know compounding is not a force to be reckoned with, compounded debt means you end up paying the bank a scary amount of money.

Therefore, if you desire Financial Freedom, use the following KISS (Keep it Simple Stupid) heuristic:

Avoid debt.

The main takeaways here are:

• Compounding is responsible for generating great wealth or great debt because of exponential growth.

• And because exponential growth feeds off of time and larger sums of money, the best ways to benefit from compounding are to:
  • Start investing early and often, e.g., by setting monthly automatic deposits to your Roth IRA or 401k
  • Have a long-term investing strategy
  • Keep your investment fees low so you keep more money
  • Avoid debt

Notes:

• Remember that all investments are subject to risk, including the possible loss of the money you invest.
• How to Teach Kids Compound Interest (youtube video)